96. 不同的二叉搜索树

#动态规划 2025-01-24

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;    
        for(int i = 1; i <= n; i++){
            for(int j = 0; j < i; j++){
                dp[i] += dp[i-j-1] * dp[j];
            }
        }

        return dp[n];
    }
};

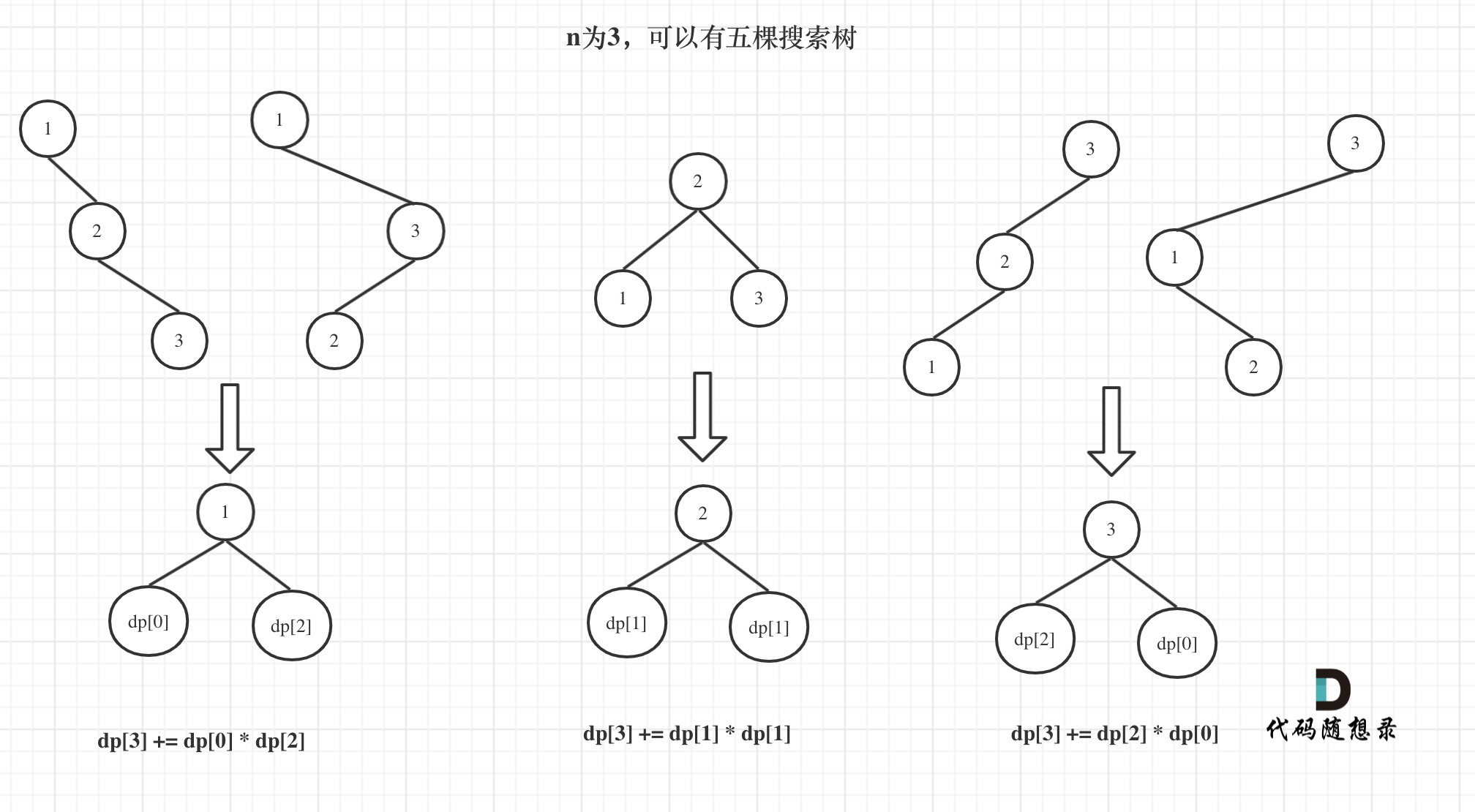
首先必然需要拿出 1 个节点作为根节点开始（确定不变的节点），因此还剩下 2 个节点可分配。存在的可能有：

左子树 2 个节点，右子树为 0 个节点
左子树 1 个节点，右子树为 1 个节点
左子树 0 个节点，右子树为 2 个节点

由于之前我们已经计算出dp[2]、dp[1]、dp[0]，这里就能直接利用起来了。一般网上分析到这点之后就会选择停止，按理讲也没问题，但我想继续深究一下：

当我们拿到节点数的时候（比方说这里的N = 3），我们必然会选择用1个节点作为根节点，其余 2 个节点拿去分配。因此 1 个节点已经被确定，2 个节点没有被确定，多样性就体现在可分配的 2个节点上，按照不同的分配来形成不同的二叉搜索树。

可是，不确定只有变成确定才能得出我们想要的结果。我们要把不确定变成确定，所以才会在上面进行各种可能的讨论，这种抽象的讨论下已经逐渐开始具体，尽管这里面还存在多样性，可你会发现这种多样性已经如泡影，在 dp 中早已有实际的记录（确定性），直接取出来用即可。

我简单举例：左子树 2 个节点，右子树为 0 个节点。

这是前面分类讨论中的一种情况，对于 0 个节点没有讨论价值，对于 2 个节点就有的说。

对于左子树的2 个节点，拿出 1 个节点作为根节点，剩余 1 个节点带来多样性（不确定），明眼人都知道这里能够制造两种可能，因此对于这棵左子树有 2 种形态（确定）。相应的，我们的 dp[2] 早就有记录了，关于节点为 2 会有多少种情况。

这就是从不确定到确定的过程，由于dp中记录着之前不确定的具体结果，拿过来用就可以了。