15. 三数之和
#双指针 2025-01-18

167. 两数之和 II - 输入有序数组

我们先用双指针解答此题，再来引出三数之和：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int left = 0;
        int right = numbers.size() - 1;
        
        while(left < right){
            int sum = numbers[left] + numbers[right];
            if(sum < target){
                left++;
            }else if(sum > target){
                right--;
            }else{
                return {left + 1,right + 1};
            }
        }
        return {};
    }
};

从题目描述来看，可以提取出几个关键信息：

  • 数组有序，因此如果两个数之和比目标值小，left++；两个数之和比目标值大，right--。
  • 返回下标，但特点是下标从 1 开始算，而不是从 0 开始。
  • 有唯一的结果，拿到第一个结果就可以选择返回。

15. 三数之和

题目没有要求返回下标，也允许按任意顺序返回，排序会让信息量增大，对我们有利。

再一个就是不要忘记去重问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> result;
        sort(nums.begin(), nums.end());

        int size = nums.size();
        if (nums[0] > 0 || nums[size - 1] < 0) // 优化而已
            return result;

        for (int i = 0; i < size - 2; i++) { // size - 2，后两个数无法与后面的数再组成三个数
            if (i > 0 && nums[i] == nums[i - 1]) {  // 去重 i
                continue;
            }

            int left = i + 1;
            int right = size - 1;
            
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                if (sum > 0) {
                    right--;
                } else if (sum < 0) {
                    left++;
                } else {
                    result.push_back({nums[i], nums[left], nums[right]});
                    while (left < right && nums[right] == nums[right - 1]) {    // 去重 right
                        right--;
                        continue;
                    }
                    while (left < right && nums[left] == nums[left + 1]) {      // 去重 left
                        left++;
                        continue;
                    }
                    // 缩减，看范围内是否还能继续匹配到
                    right--;
                    left++;
                }
            }
        }

        return result;
    }
};

数组已经排序，优化策略为如果第一个数大于 0，代表三数之后不可能等于 0，会永远大于 0；或者最后一个数小于 0，代表三数之后不可能等于0，会永远小于 0。

再谈的就是去重问题，容器中存储的结果是这三部分组成 {nums[i], nums[left], nums[right]}。因此去重就是针对这三个下标的去重。

在此之前，还是应该谈一谈寻找的思路：

image20250118123951411.png

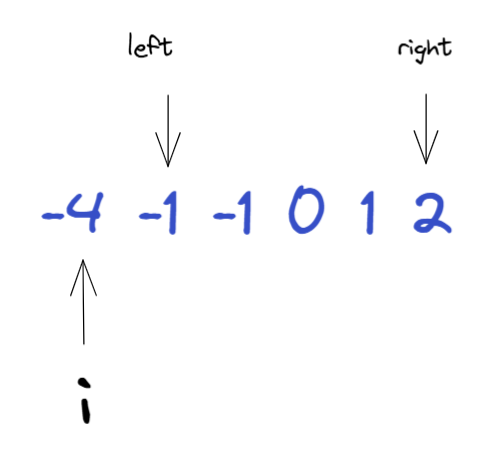
从第一个元素开始遍历，截止到倒数第三个元素（题目保证至少有三个元素），因为后面两个元素不可能有机会往后匹配组成三数之和。left 是遍历元素的后一个元素的下标，right 指向最后一个元素的下标。

left 和 right 就是在[left,right]完成匹配工作。在这个区间内匹配可能成功多次，因此是在一个循环中进行的。

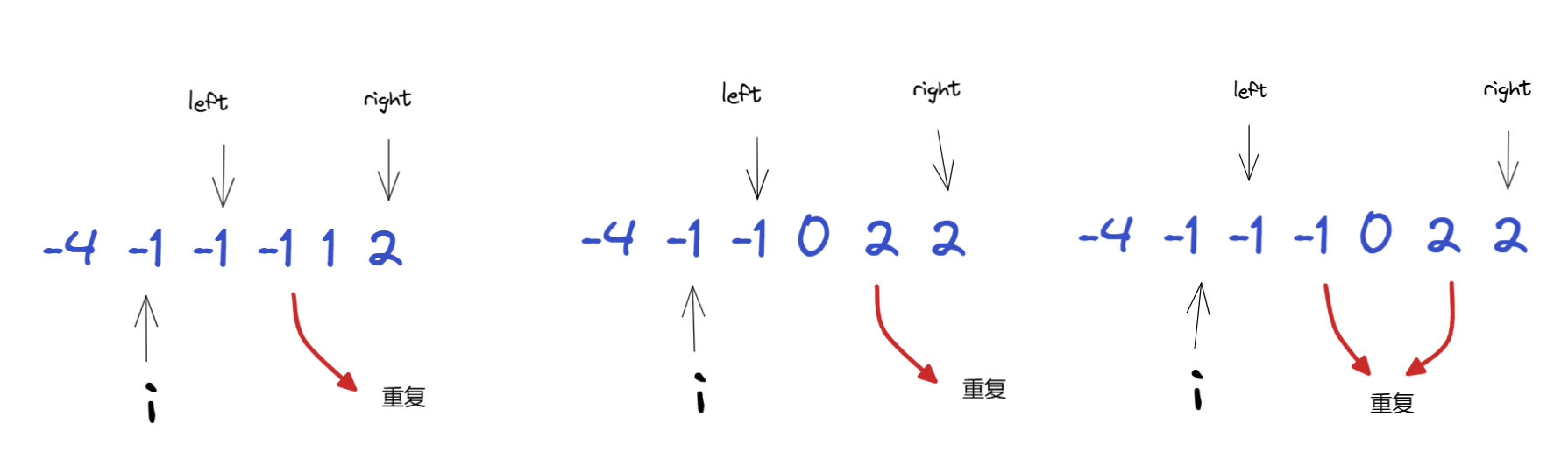
对 i 进行去重：

image20250118125252293.png

我们看图知道一定是第一个 1 第一次匹配三数之和成功，后面再出现的 1 去匹配就是重复的，我们的去重逻辑也就清晰了。

i > 0 && nums[i] == nums[i - 1]，即当前元素和前一个元素比较，如果相同就代表会重复。

left 和 right 去重：

image20250118131059842.png

我们知道，left 和 right 的去重，是在匹配成功之后进行的，这里面有种确定性地含义。假定现在 left 的右边一个元素 或者 right 的左边的一个元素是重复的， 那么不管是哪种情况，都表明三个数是具体值也都确定（首先 i 已经确定，那么 left 确定情况下 right 就确定，right 确定情况下 left 就确定，left 和 right 都确定那还有什么好说的），不然不可能构成有效的三数之和。但是我们在匹配成功之后，这个时候重复的元素只会导致三数之和是重复的，属于无效组合。因此，有必要对 left 和 right 进行去重。

匹配成功，缩减之后继续匹配：

image20250118130009934.png

因为 left 和 right 构成一个区间，很有可能会多次匹配成功，所以在去重之后继续缩减，继续进行匹配，直到退出循环。