消元
消元法是计算机软件求解线形方程组所用的最常见的方法。任何情况下,只要是矩阵
A 可逆,均可以通过消元法求得 Ax=b
的解。
高斯消元法就是通过对方程组中的某两个方程进行适当的数乘和加,以达到将某一未知数系数变为零,从而削减未知数个数的目的。
- 消元成功:矩阵的主元不包含 0, 也就是说,可逆矩阵
- 消元失败:矩阵的主元有至少一个 0,也就是说,不可逆矩阵
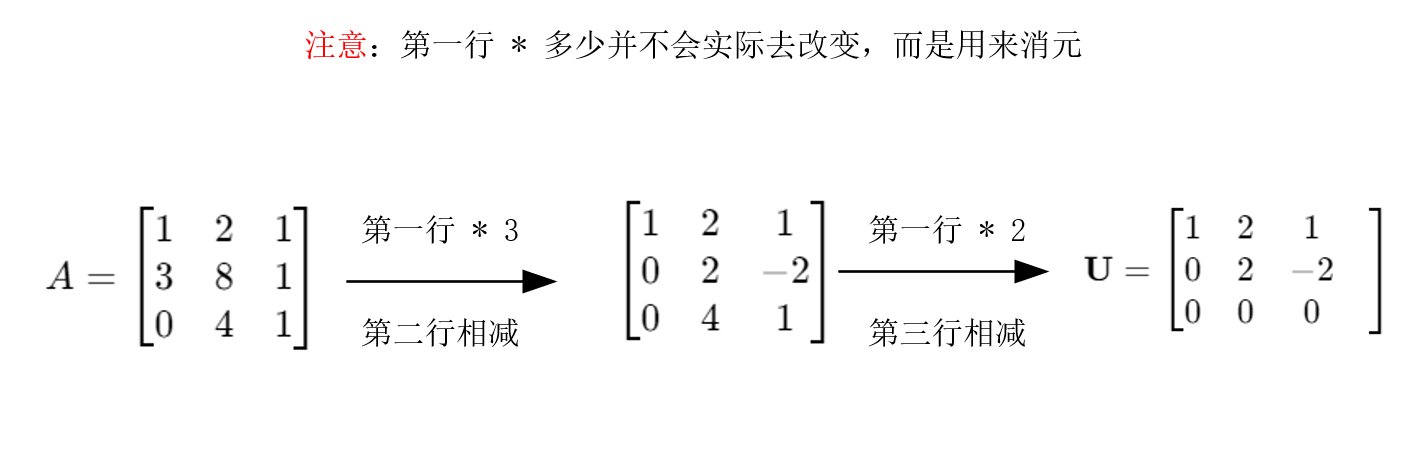
求解目标: \[ \begin{aligned}x+2y+z=2\\3x+8y+z=12\\4y+z=2\end{aligned} \] 转换成 Ax = b 形式: \[ A=\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}\mathbf{b}=\begin{bmatrix}2\\12\\2\end{bmatrix} \] 注意看这个矩阵,左上角的数字为 1,称其为“主元一”,是相当关键的。
通过消元将第一列中除了主元之外的数字均变化为0,寻找一种 U矩阵 (U upper triangular 上三角矩阵)。就像下面这种:

操作方法就是用之后的每一行减去第一行的适当倍数。
可以看到下面计算之后,证明 A 是一个可逆矩阵。
需要说明的是,主元不能为0,如果恰好消元至某行,0出现在了主元的位置上,应当通过与下方的一行进行“行交换”使得非零数字出现在主元位置上。
如果0出现在了主元位置上,并且下方没有对等位置为非0数字的行,则消元终止,并证明矩阵A为不可逆矩阵,且线性方程组没有唯一解。
回代
做方程的高斯消元时,需要对等式右侧的b做同样的乘法和加减法。手工计算时比较有效率的方法是应用增广矩阵,将 b 插入矩阵 A 之后形成最后一列,在消元过程中带着 b 一起操作。
前面介绍消元的基本思路,以后实际情况中需要将 b 插入矩阵 A 之后形成最后一列,在消元过程中带着 b 一起操作。
\[ \begin{bmatrix}1&2&1&2\\3&8&1&12\\0&4&1&2\end{bmatrix}\to\begin{bmatrix}1&2&1&2\\0&2&-2&6\\0&4&1&2\end{bmatrix}\to\begin{bmatrix}1&2&1&2\\0&2&-2&6\\0&0&5&-10\end{bmatrix} \] 等价于: \[ \begin{align*} x + 2y + z &= 2 \\ 2y - 2z &= 6 \\ 5z &= -10 \end{align*} \] z = -2,y = 1,x = 2
消元矩阵
消元矩阵,就是将前面演示的消元过程中的行变换转化为矩阵之间的乘法形式。
即用矩阵描述消元过程。
一列 乘以 一个矩阵,结果是一列
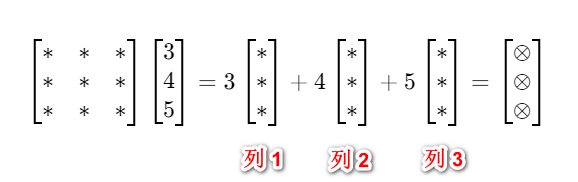
一行 乘以 一个矩阵,结果是一行

然后,我们来观察下面这个规律:
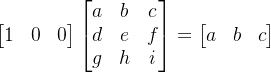
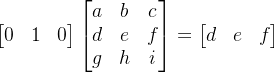
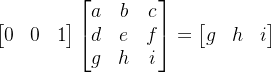
所以,如果我们的矩阵是下面这个形式,与原矩阵相乘将不会改变原矩阵,我们称呼这个矩阵为单元矩阵:
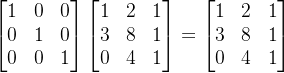
我们下面来求解左边的内容: \[ \begin{bmatrix}&&\\&&\\&&\end{bmatrix}\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix} \] 结合前面的知识,我们能很快写出第一行和第三行,因为这两行并没有变化。 \[ \begin{bmatrix}1&0&0\\&&\\0&0&1\end{bmatrix}\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix} \] 关键是看第二行: \[ [-3\quad1\quad0]\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}\quad=\quad\begin{array}{cccc}-&3&[1&2&1]\\+&1&[3&8&1]&=[0&2&-2]\\+&0&[0&4&1]\end{array} \] 即:
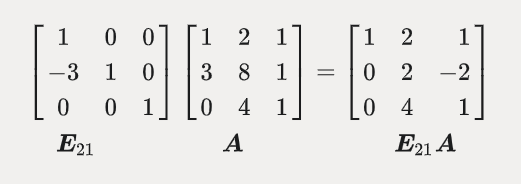
左乘的这个矩阵为称为初等矩阵(E),E21 表示将矩阵A的第2行第1列的位置变为0的消元矩阵。
接着,我们看到 E21A 第三行第二列还有个 4,要寻找一种 U矩阵 ,得将其变换为 0,见下图:
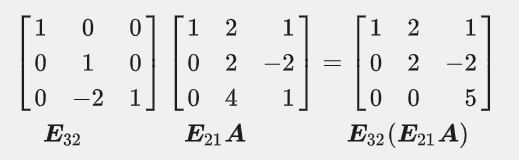
我们将这两步综合起来,即 E32(E21A) = U ,也就是说如果我们想从 A 矩阵直接得到 U 矩阵的话,只需要 E32(E21A) 即可。
你可以看到,我们这里一直是在左乘,先是 E21A,即 A 左乘一个 E21;再是 E32(E21A),即 E21A 左乘一个 E32。
之所以如此,是有个概念得讲:在一个矩阵A的左边乘一个矩阵(简称左乘),就是对 A 进行行变换,而在 A 右边乘一个矩阵(简称右乘),就是对A进行列变换。
[!NOTE]
矩阵乘法满足结合律,但不满足交换律
置换矩阵
用矩阵相乘来完成矩阵的行交换与列交换,而用到的矩阵叫做置换矩阵。
行交换: \[ {\begin{bmatrix}0&1\\1&0\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}c&d\\a&b\end{bmatrix}} \] 列交换: \[ \begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}0&1\\1&0\end{bmatrix}=\begin{bmatrix}b&a\\d&c\end{bmatrix} \] 即左乘行交换,右乘列交换。
[!CAUTION]
左右乘效果不同也展示了矩阵运算不符合交换律的性质。
逆矩阵
把一个消元结束的 矩阵 U 如何变为 未经消元的 矩阵 A 呢?即乘上一个逆矩阵! \[ [?]\begin{bmatrix}1&0&0\\-3&1&0\\0&0&1\end{bmatrix}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix} \]
就以之前的 E21 举例,这次变换是从第二行中减去三倍的第一行,那么其逆变换就是给第二行加上三倍的第一行,所以逆矩阵(上面的 ?)如下: \[ \begin{bmatrix}1&0&0\\3&1&0\\0&0&1\end{bmatrix} \] 我们把矩阵 E 的逆记作 E−1 ,所以有 E−1E = I