两方程两未知数
\[ \begin{align} 2x - y &= 0 \\ -x + 2y &= 3 \end{align} \]
转换成行矩阵,见下:AX = B
\[ \begin{bmatrix}2&&-1\\-1&&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix} \]
你可以这样看待,右边的未知数 x 和 y 已经排布好,接着就是将上边的不等式与之匹配。
第一个不等式 x 的系数为 2,y 的系数为 -1;第二个不等式 x 的系数为 -1,y 的系数为 2。x 和 y 自上而下,这些与之匹配的系数也就相应自上而下。
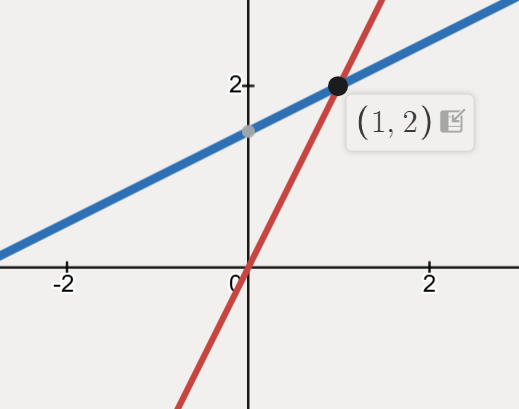
转换成列矩阵(以后就称线性组合),见下: \[ x \begin{bmatrix} 2 \\ -1 \end{bmatrix} + y \begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} \] 那么 x 和 y 为多少,才让这个等式的成立具体化呢?当 x = 1,y = 2时。
记忆还不错的你,也应该看出这里的 x = 1,y = 2 就是之前两个方程的解,即交点。
想会计算?我们看几个公式:

前面讲的计算,是指已经知晓 x 和 y 值的情况下,向量的计算规则。但如何求得 x 和 y 的值呢?还没有讲到,前面只是直接给出答案。
以原点 (0,0) 为起始点,绘制出对应的直线:
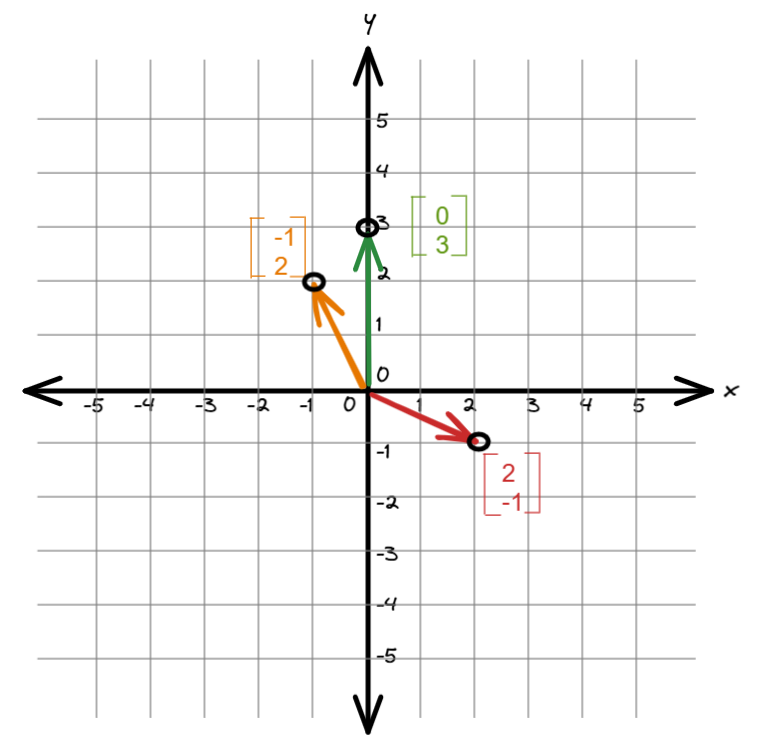
我们暂且将绿线和红线的箭头连接起来,可以看到这条黑线是黄线的两倍。
因此,我们讲 x = 1,y = 2。
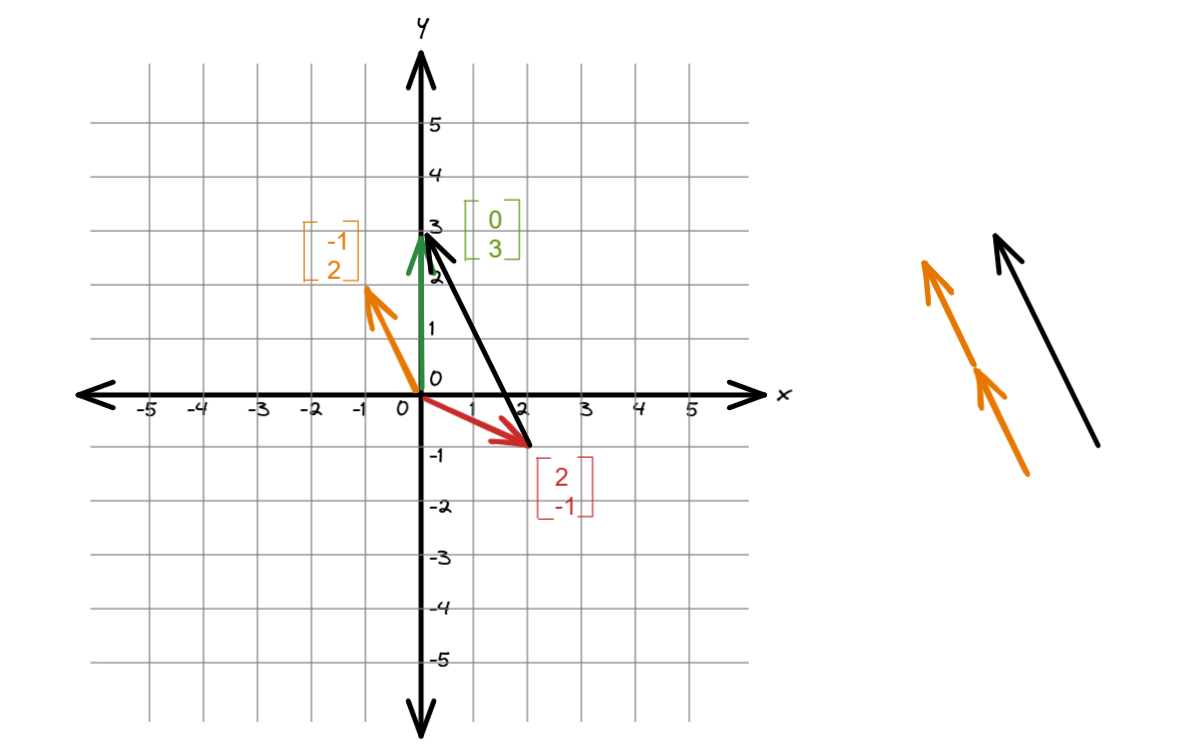
[!TIP]
图中的几种颜色且有箭头的线在数学中称之为向量,如果不明白图中向量的运算,去补充向量的运算法则
三方程三未知数
\[ \begin{align} 2x - y &= 0 \\ -x + 2y -z &= -1 \\ -3y + 4z &= 0 \end{align} \]
网站推荐:https://www.desmos.com/3d
后面学习如何求解,本节暂时无能为力,只是引出随着纬度增加,绘图的方式算不上明智之举。
矩阵相乘
Ax = b,求解 b: \[ \begin{bmatrix}2&5\\1&3\end{bmatrix}\begin{bmatrix}1\\2\end{bmatrix} \] 推荐方式,将行矩阵方式转换成列矩阵方式求解: \[ \begin{bmatrix}2&5\\1&3\end{bmatrix}\begin{bmatrix}1\\2\end{bmatrix}=1\begin{bmatrix}2\\1\end{bmatrix}+2\begin{bmatrix}5\\3\end{bmatrix}=\begin{bmatrix}12\\7\end{bmatrix} \]
x 中 第 1 个数 和 A 中 第 1 列相乘 + x 中 第 2 个数 和 A 中 第 2 列相乘 得到结果。
基于此规律,相比下次矩阵相乘也明白该怎么做了。