 4d74699c20737f2b826f13ae275e31db.png
4d74699c20737f2b826f13ae275e31db.png
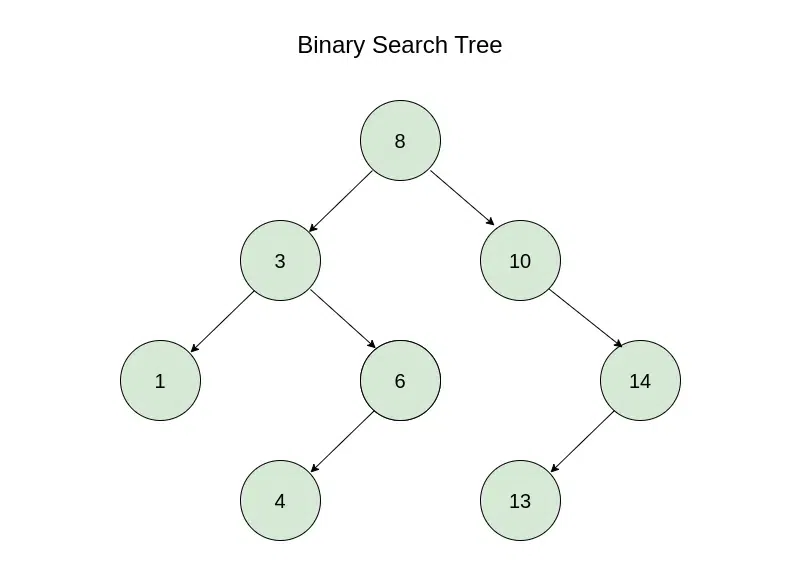
值:左子树 < 父节点 < 右子树
完整代码地址:基于二叉搜索数实现
map
基于二叉搜索树实现 map
可视化:https://www.cs.usfca.edu/~galles/visualization/BST.html
节点定义
1
2
3
4
5
6
7
8
9
10
11
12
13
| template<typename K,typename V>
struct TreeNode
{
std::pair<K,V> data;
TreeNode* left;
TreeNode* right;
TreeNode* parent;
TreeNode(const K& k,const V& v,TreeNode* parent = nullptr)
: data(std::make_pair(key,val))
, left(nullptr)
, right(nullptr)
, parent(parent) {}
};
|
搜索
从 BST 的根开始,将目标值(要搜索的值 key)与根节点的值进行比较:
- 如果目标值等于根节点的值,返回 data
- 如果目标值小于根节点的值,则向左递归,因为较小的值位于 BST
的左子树上
- 否则,如果目标值大于根节点的值,则向右递归,因为较大的值位于 BST
的右子树上
- 重复上面的步骤,直到无法再遍历为止
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| TreeNode<K, V> *find( const K &target )
{
TreeNode<K, V> *find_node = root;
while ( find_node )
{
auto cur = find_node->data.first;
if ( target < cur )
{
find_node = find_node->left;
} else if ( target > cur )
{
find_node = find_node->right;
} else {
return find_node;
}
}
return(nullptr);
}
|
插入
遍历树,通过将要插入的值(目标值)与当前节点的值进行比较来找到插入点:
- 如果目标值小于当前节点的值,则移动到左子树
- 如果目标值大于当前节点的值,则移动到右子树
- 重复上述步骤,直到到达叶子节点
插入具有目标值的新节点。如果目标值小于父节点的值,则将其插入到左侧,否则插入到右侧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| void insert( const K &key, const V &val )
{
auto new_node = new TreeNode<K, V>( key, val );
if ( root == nullptr )
{
root = new_node;
return;
}
TreeNode<K, V> *cur = root;
TreeNode<K, V> *parent = nullptr;
while ( cur )
{
auto cur_key = cur->data.first;
parent = cur;
if ( key < cur_key )
{
cur = cur->left;
} else if ( key > cur_key )
{
cur = cur->right;
} else {
root->data.second = val;
return;
}
}
if ( key < parent->data.first )
{
parent->left = new_node;
} else {
parent->right = new_node;
}
new_node->parent = parent;
}
|
删除(考虑三种情况)
第一种情况:删除叶子节点
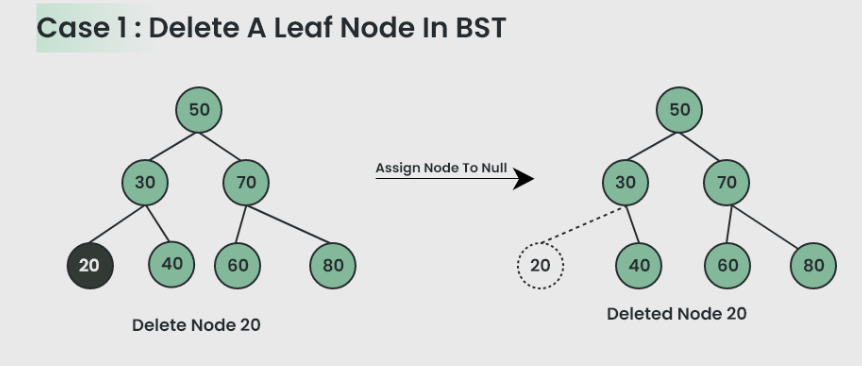 image20250114185035746.png
image20250114185035746.png
第二种情况:删除的节点有单个节点
[!WARNING]
通过更改指针的指向彻底删除节点(节点位于树中,不是单纯 delete
然后置为 nullptr),不要忘记更新相关节点的成员变量信息。
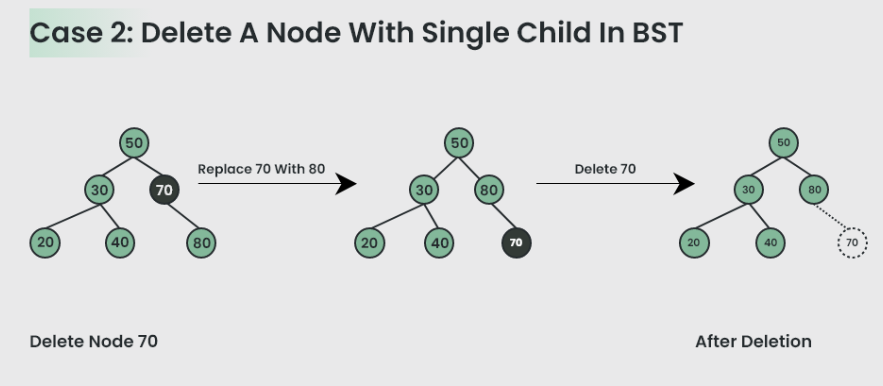 image20250114185058590.png
image20250114185058590.png
第三种情况:删除的节点有两个节点
[!WARNING]
降级为叶子节点进行处理,不要忘记更新相关节点的成员变量信息。
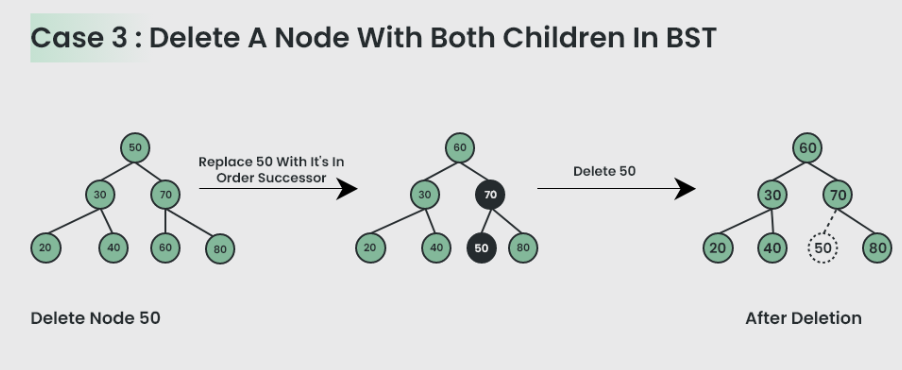 image20250114185121141.png
image20250114185121141.png
[!WARNING]
上面的三种删除情况,务必考虑删除节点为根节点的情况。
从根节点开始,寻找目标节点(要删除的节点),如果目标节点小于当前节点则向左移动,如果目标节点大于当前节点则向右移动。重复此步骤,直到找到目标节点或到达空节点。
当找到目标节点时,处理以下3种情况进行删除:
- 如果目标节点是叶子节点,只需将其删除
- 如果目标节点有 1
个子节点,则用其子节点替换目标节点并删除目标节点
- 如果目标节点有 2 个子节点
- 找到目标节点的右子树中最小的节点(或左子树中最大的节点),我这里选择右子树中最小的节点
mininum
- 将目标节点替换为 mininum
- 已经降级为叶子节点,按照前面叶子节点方式处理即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| void erase( const K &key )
{
if ( root == nullptr )
return;
TreeNode<K, V> *target = find( key );
if ( target == nullptr )
return;
if ( target->left && target->right )
{
TreeNode<K, V> *successor = mininum( target->right );
target->data = successor->data;
target = successor;
}
TreeNode<K, V> *child = target->left ? target->left : target->right;
TreeNode<K, V> *parent = target->parent;
if ( child )
{
child->parent = parent;
}
if ( parent )
{
parent->left == target ? parent->left = child : parent->right = child;
}else{
root = child;
}
delete target;
target = nullptr;
}
|
中序后继节点
首先要确定中序遍历的后继:
- 如果该节点有右子节点,
那么后继是其右子节点的子树中最左端的节点(就是之前我们实现找右子树中最小值的那种方法)
- 如果该节点没有右子节点, 那么后继是离它最近的祖先,
该节点在这个祖先的左子树内
 b545036afb4fb8ed3d3425f287bec91.png
b545036afb4fb8ed3d3425f287bec91.png
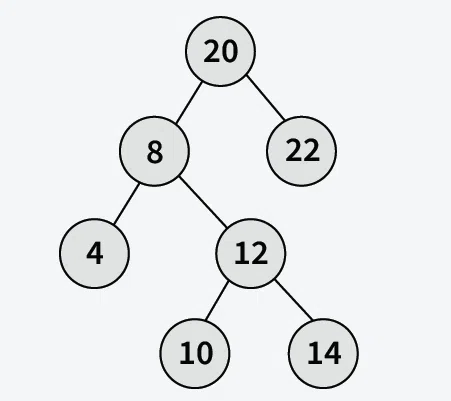
如图所示:8 的中序后继为 10,10 的中序后继为 12,14 的中序后继为
20。
我们都知道,二叉搜索树的中序遍历是有序的:4,8,10,12,14,20,22。
这时候你就明白 中序后继 的含义,你自己看,8 后面的一个节点是
10,因此我们讲 8 的中序后继为 10。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| TreeNode<K, V> *mininum( TreeNode<K, V> *node )
{
while ( node->left != nullptr )
{
node = node->left;
}
return node;
}
TreeNode<K, V> * Inorder_Successor( TreeNode<K, V> *node )
{
if ( node->right )
{
return mininum( node->right );
}
TreeNode<K, V> * parent = node->parent;
while ( parent && parent->left != node )
{
node = parent;
parent = parent->parent;
}
return parent;
}
|
推荐文章
Binary
Search Tree in C++