491. 非递减子序列
#回溯 2024-09-20 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
public:
      void backtrace(vector<int>& nums, int cur){
        if(path.size() >= 2){
            result.push_back(path);
        }
        set<int> removeSame;
        for(int i = cur; i < nums.size(); i++){
            if(!path.empty() && path.back() > nums[i]){     // 非递增
                continue;
            }
            if(removeSame.find(nums[i]) != removeSame.end()){   // 有重复
                continue;
            }

            // 到达这里的，皆是合法的
            removeSame.insert(nums[i]);
            path.push_back(nums[i]);
            backtrace(nums,i + 1);
            path.pop_back();
        }
      }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrace(nums,0);
        return result;
    }
};

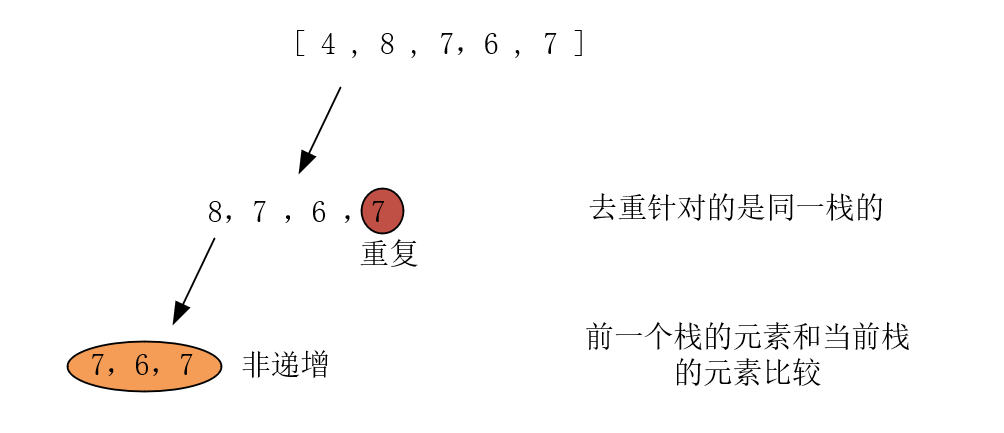
这道题真的困扰好久，我觉得就是没有去画图，导致在脑子里来回绕，特画如下简图：

491.非递增子序列.png

我们先解决非递增问题。前一个栈的元素 A 和当前栈的所有元素逐一比较，如果谁比 A 大，那么这个数就是不合法的，将被跳过。合法的就会继续往下判断。

接着处理重复元素的问题，从图中明显看得出是同一栈中的元素重复了，那就只需要维护一个当前栈的一个记录项（这里用的 set）即可，当它进入下一个栈时就会被清空。因此，只需要让检查当前栈的元素是否存在与 set 集合中，存在就意味着是不合法的。因此removeSame.insert(nums[i])，即加入当前栈且合法的元素进去，以便后续去重。

还要path.push_back(nums[i])，因为合法的元素是要加入到 path 中记录的，这也是我们的最终目标的组成部分。

来到末尾，从题意中可以看到的是，我们是要在合法元素的下一个位置开始，因此 backtrace 的第二个参数是 i + 1。可不要误写成为 cur + 1。