第六章：惰性求值
#函数式编程 2024-09-10

假定现在需要对 A 和 B 进行求值，但问题是后面可能未必需要用到，这就白白浪费 CPU 时间去计算它了。也许可以用 Lambda 表达式，等需要的时候调用函数 P 来获取乘积结果。

1
2
3
auto P = [A,B] {
  return A * B;  
};

对于一个可能不需要结果的复杂的计算，这样做就是对代码的优化。但也带来了新的问题：如果这个值不止一次被使用怎么办？使用这种方法，每次调用都要计算这个值。更好的做法是在第一次计算该值时，将它保存起来。

这就是“惰性”的全部意义：对于工作不是提前而是尽可能推后。因为有惰性，也不可能多次重复做一件事，所以当得到结果后，就应记住这个结果。

惰性作为一种优化技术

集合惰性排序

假设有几百个员工信息存储在一个向量中，一个窗口一次可以显示其中的 10 名员工。用户可根据姓名、年龄和工龄等多种标准对员工进行排序。当用户选择按年龄对员工进行排序时，程序应显示 10 个年龄最大的员工，并且允许用户向下滚动，查看剩余的部分。

用快速排序算法，找到合适的基准元素，对基准前面的元素进行递归排序，对基准后面的元素暂时不进行递归排序。

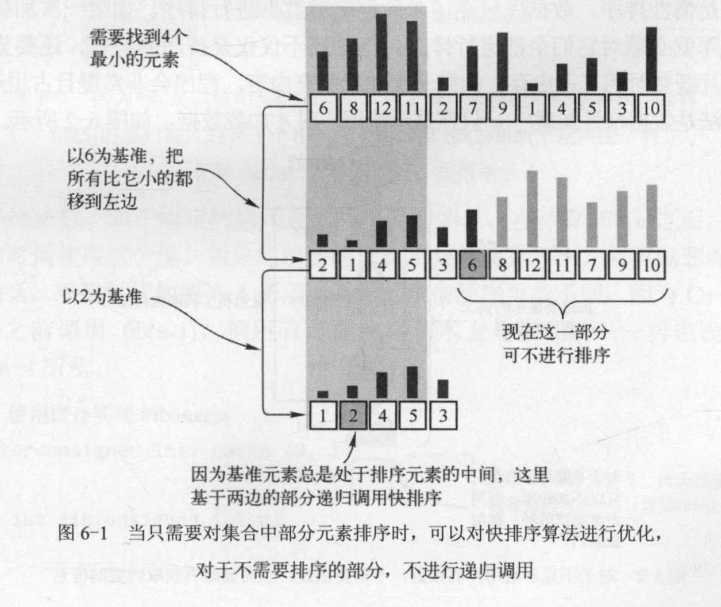
快速排序.png

通过缓存函数结果修剪递归树

C++ 虽然不直接支持惰性求值，但可以根据自己的意愿进行实现。对于不同的情况决定如何实现惰性求职。看一个常见的例子：

斐波拉契数列.png

这种实现是低效的，因为有很多重复的计算，见下图：

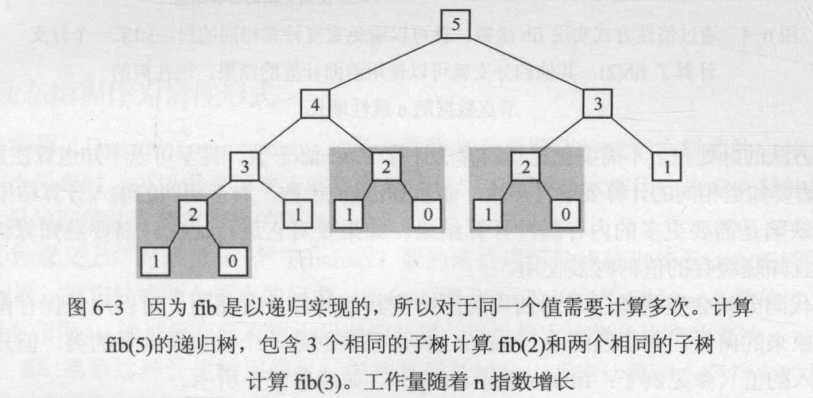
重复计算.png

该函数是纯函数，对于给定的输入总返回相同的结果。在计算 fib(n) 之后，可以保存起来，在需要的时候使用这个值。如果把前面的计算结果都缓存起来，就可以删除所有重复的子树。

1
2
3
4
5
6
7
8
9
10
11
12
std::vector<unsigned int> cache {0, 1};

unsigned int fib(unsigned int n)
{
    if (cache.size() > n) {
        return(cache[n]);
    } else {
        const auto result = fib(n - 1) + fib(n - 2);
        cache.push_back(result);
        return result;
    }
}

效果如下图：

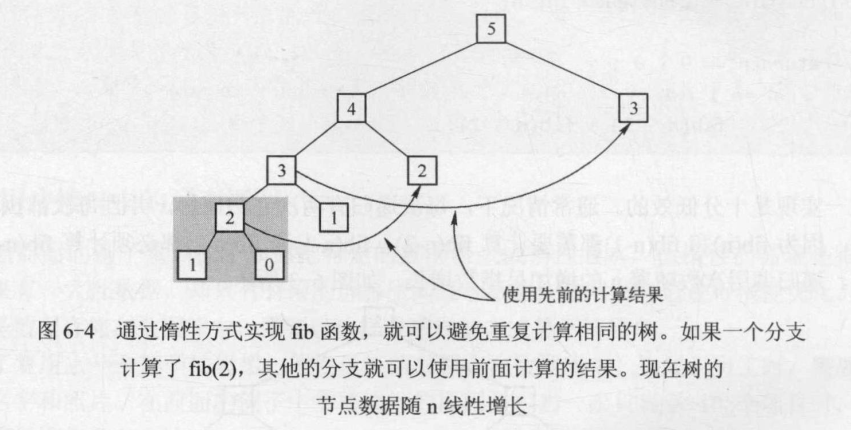
缓存.png

实际上这里还可以继续优化，因为本质上计算当前值，只需要利用前面两个值的结果就行，意味着不需要每次计算都存储一个计算结果，这会导致空间越来越大，实际上只需要存储两个元素的空间大小即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
unsigned int fib(unsigned int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;

    unsigned int prev1 = 0;
    unsigned int prev2 = 1;

    for (unsigned int i = 2; i <= n; ++i) {
        unsigned int current = prev1 + prev2;
        prev1 = prev2;
        prev2 = current;
    }

    return prev2;
}

动态规划作为惰性形式

如果你了解动态规划，就明白之前的案例已经就是动态规划的思想，尽管那不是动态规划的写法。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int fib(int n) {
        if(n <= 1) return n;
        vector<int> result(n+1);
        result[0] = 0;
        result[1] = 1;
        for(int i = 2; i <= n; i++){
            result[i] = result[i - 1] + result[i-2];
        }
        return result[n];
    }
};

通用记忆化

对于不同的问题单独编写自定义缓存是比较好的，这样就可以控制特特定值在缓存中的存放时间，并且可以确定最好的缓存结构，但有时把一个函数进行包装，而得到该函数的记忆化版本会比较好。

如果不知道函数的调用参数，那么通用的缓存就是 map。任何纯函数都是从参数到值得映射，因此这种缓存可毫无问题地适应任何纯函数。

函数指针记忆化.png

如果要对递归函数记忆化，最好缓存它的最后结果，而不是递归结果，因为递归调用是调用的原函数，而不是记忆化的包装函数。

表达式模板与惰性字符串拼接

考虑多个字符串拼接，见下图：

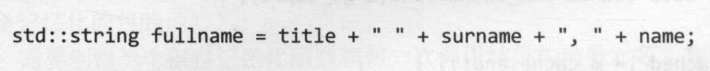
字符串拼接1.png

虽然能够实现字符串拼接，但是这样效率低效。因为没有提前分配内存大小，导致没拼接一次就要进行扩容拷贝操作。

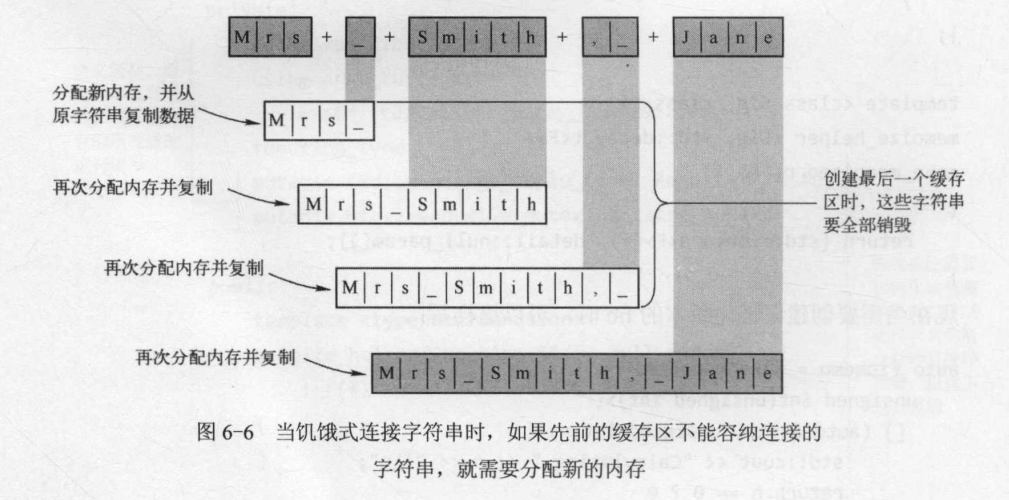
字符串拼接2.png

这正是表达式模板起作用的地方：它们允许产生表达式的定义，而不是求解表达式的值。不是实现操作符 + 拼接字符串，而是返回表达式表示的定义，后面再对它进行计算。在这个例子中，问题的根源在于操作符 + 是一个二元操作符，却要实现多次字符串拼接。因此，需要创建一个表示拼接多个字符串的结构。因为需要存储任意数目的字符串，所以创建一个递归结构模板比较合适：一个节点保存单个字符串（data成员），另一节点保存剩下的所有字符串（tail成员）。

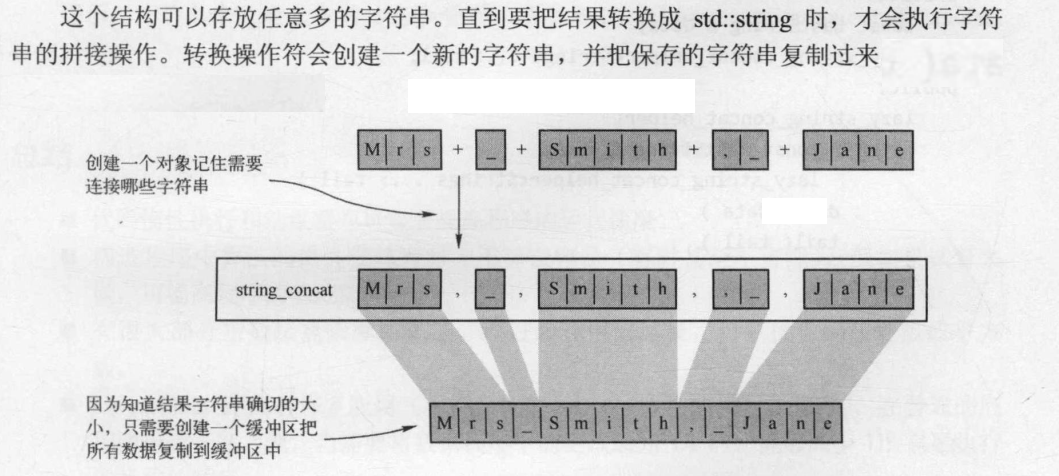
字符串拼接3.png

表达式模板是一种迟延计算的强大工具。它们经常用在操作矩阵的库中，或在提交编译器之前对表达式进行优化的场合。

⭐️内容取自译者程继洪、孙玉梅、娄山佑《函数式编程》，仅从中取出个人以为需要纪录的内容。不追求内容的完整性，却也不会丢失所记内容的逻辑性。如果需要了解细致，建议读原书。