第二章：函数式编程之旅

第二章：函数式编程之旅

#函数式编程 2024-08-16

• 函数使用函数
• STL实例
  • 求平均值
  • 折叠
  • 删除字符串空白符
  • 基于谓词分割集合
  • 过滤和转换
• STL算法的可组合性
• 编写自己的高阶函数
  • 接收函数作为参数
  • 用循环实现
  • 递归和尾调用优化
  • 使用折叠实现

函数使用函数

所有函数式编程语言的主要特色就是函数可被看作一个普通的值。它们可被存储于变量中，放到集合或结构中，作为参数传递给其他函数，并可以作为其他函数的返回结果中。能够接收函数作为参数或返回函数作为结果的函数称为高阶函数。

我们来看一个实例：假设有一组人，需要写出组内所有女性的名字。如下图所示。

也就是说组内由男性和女性组成，先要把男性过滤掉而剩下女性（过滤），然后获取这些女生的名字（转换）。

这里使用的首个高阶结构是集合过滤。通俗地讲，过滤是一个简单的算法，它主要检查原集合中的每个条目是否满足一定的条件。如果满足，则该条件被放入结果集中。过滤算法并不能事先知道用户对他们的集合使用什么样的谓词函数进行过滤。过滤可以针对一个特定的属性（如本例中的性别属性的值），也可以同时针对多个属性（如找到所有黑头发的女性），或更复杂的过滤条件（获取最近购买新车的所有女性）。因此，这种结构必须提供一种方法，可以让用户指定所需的谓词。在这个例子中，这个结构需要提供一个接收人的谓词，并返回这个人是不是女性。因为过滤允许传递一个谓词函数，按照定义，它是一个高阶函数。如果想从 STL 中找到具体的例子，常用的 sort 的第三个参数接受谓词，用户可以自实现谓词来筛选集合中的元素满足条件的情况下返回，比方说集合中所有元素从小到大进行排序。

过滤任务完成后，还有获取姓名的任务。需要一个结构，它接收一组人并可返回他们的名字。与过滤类似，这个结构也不能事先知道要从原集合中选取哪些值。用户可能想获取一个特定的属性(如这个例子中的姓名)、多个属性组合(可能需要找到姓和名并把它们拼接起来)，或更复杂的操作(获取一个人的所有孩子)。同样，这个结构也需要允许用户指定一个函数，从集合中获取一个条目，对条目进行某些操作，并返回一个值，把这个值放在结果集中。请注意，输出集合没必要与输入集合包含相同的类型（这一点与过滤不同）。这种结构称为映射（map）或转换（transform）。

STL实例

STL 中有很多高阶函数，这里简单介绍几个，后续有可能会单独写一篇实践常用的 STL 中提供的高阶函数

求平均值

std::accumulate 用来求和，其中：

• first 和 fast 代表容器的起始迭代器和结尾迭代器
• init 指定累加器的初始值
• 二元运算符，用于指定累加操作的类型。如果不指定，默认为加法（二进制操作将类型为T的元素（即 init）作为第一个参数，将范围内的元素作为第二个参数，并返回可以分配给类型T的值）

template <class InputIterator, class T>  
T accumulate (InputIterator first, InputIterator last, T init);

template <class InputIterator, class T, class BinaryOperation>   
T accumulate (InputIterator first, InputIterator last, T init,BinaryOperation binary_op);


// 等价于

{
  while (first!=last) {
    init = init + *first;  // or: init=binary_op(init,*first) for the binary_op version
    ++first;
  }
  return init;
}

不指定函数对象的实践代码。

#include <iostream>
#include <vector>
#include <numeric>
using namespace std;
int main() {

  vector<int> s = {2,1,0,25,-32,78,-21,-10,21};
  int result = 0;
  result = std::accumulate(s.begin(),s.end(),0);

  std::cout<<"result = "<<result<<std::endl;

  return 0;
}
/*
	result = 64
*/

指定函数对象的实践代码，使用了乘法运算符 std::multiplies<int>()，计算了所有元素的乘积。

本质上是将 init 和 容器中每一个元素逐一相乘，如下代码含义为 2 * 1 * 2 * 3 * 4 * 5。

#include <iostream>
#include <vector>
#include <numeric>
using namespace std;
int main() {

  vector<int> s = {1,2,3,4,5};
  int result = 0;
  result = std::accumulate(s.begin(),s.end(),2,std::multiplies<int>());
    
   /*
   	等价于
   	  result = std::accumulate(s.begin(),s.end(),2,[](int a,int b){
    	return a * b;
 	 });
   */

  std::cout<<"result = "<<result<<std::endl;

  return 0;
}

/*
	result = 240
*/

折叠

std::accumulate 算法是折叠的一种实现。这是一个高阶函数，它提供了对递归结构，如向量、列表和树等的遍历处理，并允许逐步构建自己需要的结果。

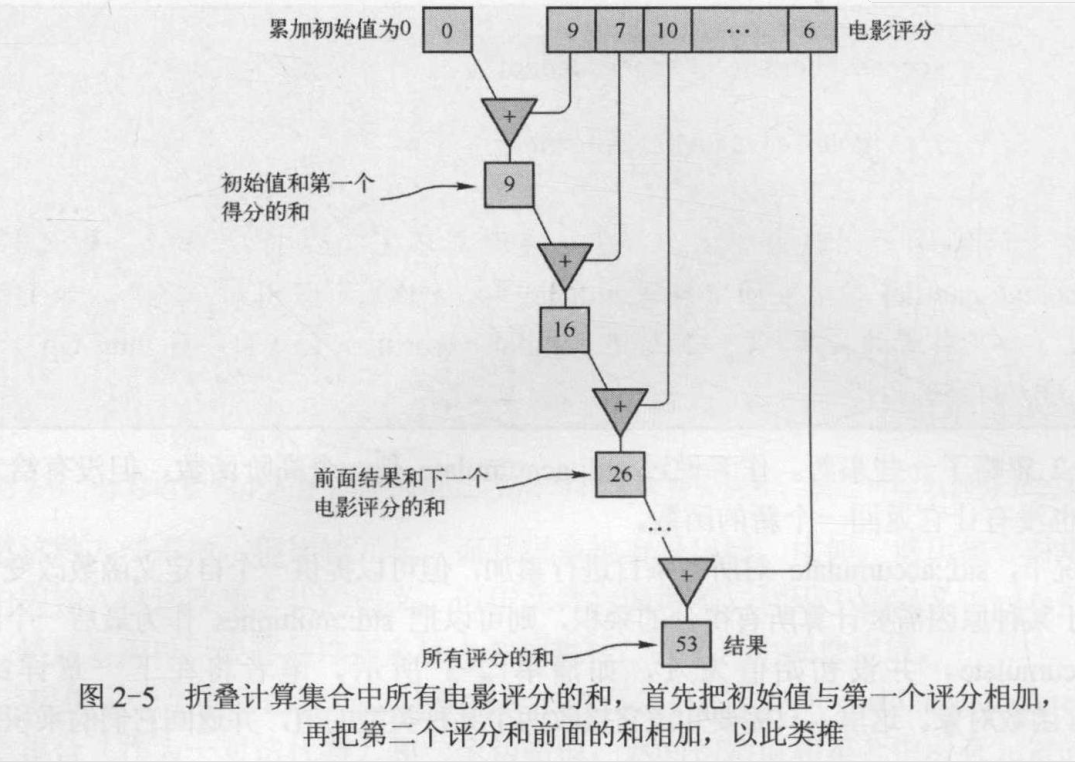
上面关于 std::accumulate 的实践代码，会让大家决定 init 的类型 要和 容器中元素的类型相同，实际上并没有这个要求，类型可以不同。下面的代码中，我们统计字符串 data 中字母的个数。

#include <iostream>
#include <vector>
#include <numeric>
using namespace std;
int main() {

  std::string data = "www.baidu.com";
  auto result = std::accumulate(data.begin(),data.end(),0,[](int count,char c){
    if (isalpha(c)){
      count++;
    }
    return count;
  });

  std::cout<<"result = "<<result<<std::endl;

  return 0;
}

/*
	result = 11
*/

折叠中有两种类型，一种是左折叠（从左往右开始遍历元素），一种是右折叠（从右往左开始遍历元素）。前面都是左折叠，C++ 也没有也没有提供独立的右折叠算法，但是我们可以通过传递反向迭代器来实现右折叠算法（crbegin 和 crend）。

删除字符串空白符

std::find_if：查找集合中第一个满足指定谓词的元素。

template <class InputIterator, class UnaryPredicate>   
InputIterator find_if (InputIterator first, InputIterator last, UnaryPredicate pred);

//等价于

{
  while (first!=last) {
    if (pred(*first)) return first;
    ++first;
  }
  return last;
}

下面演示删除一个字符串左右两边的空白。

#include <iostream>
#include <vector>
#include <numeric>
using namespace std;

std::string trim_left(std::string str){
  str.erase(str.begin(),std::find_if(str.begin(),str.end(),[](char c){
    return !isspace(c);
  }));
  return str;
}

std::string trim_right(std::string str){
  str.erase(std::find_if(str.rbegin(),str.rend(),[](char c){
    return !isspace(c);
  }).base(),str.end());
  return str;
}

int main() {

  std::string data = "   www.baidu.com   ";

  std::cout<<trim_right(trim_left(data));

  return 0;
}

/*
	www.baidu.com
*/

std::find_if 返回值为满足条件的所处位置的迭代器。trim_right 有用到 反向迭代器，.base() 返回的是反向迭代器的正向迭代器，指向找到的非空白字符的下一个位置。

基于谓词分割集合

在学习更多知识之前，假设有一个人的集合，需要把所有女性移到集合的前面。为了实现这一功能，可以使用 std::partition 和它的变体 std::stable_partition（相较于std::partition，可以保持集合中原来的顺序）。

template <class ForwardIterator, class UnaryPredicate>  
ForwardIterator partition (ForwardIterator first,ForwardIterator last, UnaryPredicate pred);


template <class BidirectionalIterator, class UnaryPredicate>  
BidirectionalIterator stable_partition (BidirectionalIterator first,BidirectionalIterator last,UnaryPredicate pred);

两个算法都接收一个集合和一个谓词。它们对原集合中的元素进行重排，把符合条件的与不符合条件的分开。符合谓词条件的元素移动到集合的前面，不符合条件的元素移动到集合的后面。算法返回一个迭代器，指向第二部分的第一个元素(不符合谓词条件的第一个元素)。返回的迭代器和原集合开头的迭代器配合，获取集合中满足谓词条件的元素(构成的集合)，与原集合尾端迭代器配合，可获得原集合中不符合谓词条件的元素(构成的合)。即使这些集合中存在空集合也是正确的。

int main() {

  vector<int> data = {1,7,-2,10,-10,43,55,-99,-89};
  auto its = std::partition(data.begin(),data.end(),[](int num){
    return num > 0;
  });

  std::cout<<"正数集合 = ";
  auto itBegin = data.begin();
  for (; itBegin != its ; itBegin++) {
    std::cout<< *itBegin << " ";
  }

  std::cout << std::endl;

  std::cout<<"负数集合 = ";
  for (; its != data.end(); its++) {    
    std::cout<< *its << " ";
  }
  
  return 0;
}

/*
	正数集合 = 1 7 55 10 43 
	负数集合 = -10 -2 -99 -89 
*/

可以看到 std::partition 返回的迭代器 its 就是一个分界线，data.begin() ~ its 是符合条件的元素，its ~ data.end() 是不符合条件以外的元素。

还有明显看到输出没有保持顺序性，只需要把 std::partition 替换成 std::stable_partition 即可。

正数集合 = 1 7 10 43 55 
负数集合 = -2 -10 -99 -89

过滤和转换

template <class ForwardIterator, class UnaryPredicate>  
ForwardIterator remove_if (ForwardIterator first, ForwardIterator last, UnaryPredicate pred);

template <class InputIterator, class OutputIterator, class UnaryPredicate>  
OutputIterator copy_if (InputIterator first, InputIterator last, OutputIterator result, UnaryPredicate pred);

remove_if 删除指定范围内满足条件的元素，对容器会有改动。

copy_if 复制指定范围内满足条件的元素到另一个容器中，对容器不会有改动。

int main() {
  std::vector<int> data = {1,7,-2,10,-10,43,55,-99,-89};

  // 复制负数到 Fdata
  std::vector<int> Fdata;
  std::copy_if(data.begin(), data.end(), std::back_inserter(Fdata), [](int num) {
    return num < 0;
  });

  std::cout << "复制负数到指定容器中 = ";
  for (int i : Fdata) {
    std::cout << i << " ";
  }
  std::cout << std::endl;

  // 移除 data 中的负数
  auto it = std::remove_if(data.begin(), data.end(), [](int num) {
    return num < 0;
  });
  data.erase(it, data.end());

  std::cout << "移除容器中负数后 = ";
  for (int i : data) {
    std::cout << i << " ";
  }
  std::cout << std::endl;

  return 0;
}
/*
	复制负数到指定容器中 = -2 -10 -99 -89 
	移除容器中负数后 = 1 7 10 43 55 
*/

std::copy_if 和 std::back_inserter ：使用 std::back_inserter 可以直接将元素追加到 Fdata 中，因此不需要手动调整容器大小。

std::remove_if 和 erase：在 std::remove_if 后，通过 erase 函数真正删除负数元素，因为 std::remove_if 是把移除的元素放到后面并没有真正移除。

STL算法的可组合性

基于 STL 的实现会生成不必要的 people 集合的副本（这是一个耗时的操作，甚至可能在拷贝构造函数被删除或私有时被禁用），并且会创建一个实际上并不需要的附加向量。为了解决这些问题，可使用引用或指针而不是副本，或者创建一个智能的迭代器，它可跳过所有不是女性的人员等。但这些额外的工作表明STL在这场战斗中已经输了，手写循环更好、更省力。

虽然标准的算法提供了一种编写函数式风格代码的方式，而没必要手动编写循环和分支，但它们并没有设计成其他函数式编程库或语言一样的可组合的。后续使用 range 可以有所改观，到时候再谈。

编写自己的高阶函数

接收函数作为参数

在 C++ 中，许多东西的行为类似于函数，但没有通用的类型用于存放类似函数的东西，而不损害程序的性能。可以把函数类型用作模板参数，让编译器在编译时确定具体的类型，而不是猜测哪种类型更好：

template <typename FilterFun>
std::vector<std::string> names_for(
	const std::vector<person_t> & people,
	FilterFun filter);

这将允许用户传递任何类似函数的东西作为参数，可以向普通的函数一样调用它。

用循环实现

几乎所有的STL算法都是由循环实现的，当你决定自己实现某个算法需要考量这样做的必要性，否则应该使用STL算法。这有几个原因。首先是简单。使用别人的代码节省时间。这也就引出了第二个好处：正确性。如果同样的东西写了一遍又一遍，一时疏忽产生错误也理所当然。STL经过了严格的测试，对于任何输入都能正常工作。基于同样的原因，使用硬编码循环实现的常用函数（我们自己实现的），也必须通过测试。

虽然很多STL算法不是纯的，但它们被设计成高阶函数，这样它们就更通用，适用于更多的场合。如果某些东西被经常使用，它也不太可能包含前面不可见的缺陷。

递归和尾调用优化

前面的解决方案从外面看是“纯”的，但具体的实现却不是。当发现一个新的符合条件的人员时，它就要修改结果向量。在纯函数式编程语言中是不存在循环的，遍历集合的函数通常是由递归实现的。本书并不深入研究递归，因为读者并不常用到它，但需要说明一些重要的东西。

对于一个非空向量，可以递归地处理它的头（第一个元素）和尾（所有其他元素），这又可以被看作一个向量。如果头满足谓词，则把它包含在结果中。如果接收到一个空向量，则什么也不需要处理，也就返回一个空向量。

这种实现是低效的。首先，由于某种原因导致向量的 tail 函数不存在：它需要创建一个新向量并将旧向量中的所有数据复制到其中（第一个元素除外）。tail 函数的问题可用一对迭代器代替向量作为输入来解决。在这种情况下，获取向量尾变得很简单–只需要移动迭代器，使它指向第一个元素即可如下图所示。

这种实现的第二个问题是，把元素插入在向量的前端。这种情况并不多。在硬编码的循环中使用添加，在向量连接时，比前置(插入)更高效。最后也可能是最重要的问题是如果集合大量调用这个函数，可能会出现问题。每次递归都要占用堆栈中的内存，如果堆栈溢出则程序崩溃。即使集合不够大，不会导致堆溢出，但函数调用也要付出代价，简单的循环比它更高效。

虽然前面的问题容易解决，但这个不同。这里需要依赖编译器把递归转换成循环。为了让编译器进行转换，必须实现称为尾递归的形式。在尾递归中，递归调用是函数的最后一件事情：递归后不能做任何事情。

尾递归函数是一种递归函数，其中递归调用发生在函数的最后一步。在尾递归中，递归调用之后不再需要执行任何其他操作，因此可以直接返回递归调用的结果。尾递归函数的一个重要特性是，它可以被编译器或解释器优化为迭代形式，从而节省栈空间，避免递归调用过深导致的栈溢出。

普通递归

int factorial(int n) {
    if (n == 0) {
        return 1;
    } else {
        return n * factorial(n - 1);
    }
}

尾递归

int factorial_tail(int n, int acc = 1) {
    if (n == 0) {
        return acc;
    } else {
        return factorial_tail(n - 1, n * acc);
    }
}

普通递归的实现中，factorial(n - 1) 的结果需要与 n 相乘，然后才返回给上层调用，因此这不是尾递归。

在尾递归的实现中，递归调用 factorial_tail(n - 1, n * acc) 是函数的最后一步操作，并且将累积的结果通过 acc 参数传递下去。这里没有其他操作依赖于递归调用的返回值，因此这是尾递归。

递归是一种强大的机制，可以让用户在不支持循环的语言中实现循环。但递归仍然属于低水平的结构。可以通过递归实现内部的“纯洁”性，但在许多情况下这样做没有意义。递归，就像手写循环，有它的一席之地。但在C++中，代码评审时就会出现问题。需要C++函数式编程检查它的正确性，并且保证在所有情况下都不会堆栈溢出。

使用折叠实现

前面已经见过折叠，但还没有从根本上理解它。折叠（Folding）一次取得一个元素，并对以前积累的值（是一个集合）和当前元素施加指定的函数，产生一个新的累积值。实质上，折叠只不过是编写尾递归函数遍历集合的一种更好的方式。共同的部分被抽取出来，用户只需要指定集合、初始值和必需的累加处理过程，而没必要编写递归函数。

---

⭐️内容取自译者程继洪、孙玉梅、娄山佑《函数式编程》，仅从中取出个人以为需要纪录的内容。不追求内容的完整性，却也不会丢失所记内容的逻辑性。如果需要了解细致，建议读原书。