142.环形链表II
#链表 2024-08-07 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {  
public:  
    ListNode* detectCycle(ListNode* head) {  
        if (head == NULL || head->next == NULL) {  
            return nullptr;  
        }  
        // 快慢指针，有环必相遇  
        ListNode* node = head;  
        ListNode* slow = head;  
        ListNode* fast = head;  
        while (fast != nullptr && fast->next != nullptr) {  
            slow = slow->next;  
            fast = fast->next->next;  
            if (slow == fast) { // 有环  
                while (true) {  
                    if (node == slow) {  
                        return slow;  
                    }  
                    node = node->next;  
                    slow = slow->next;  
                }  
            }  
        }  
        return nullptr;  
    }  
};

此题建立在你已经完成 《141.环形链表》题目，我们重点就关注判断有环之后如果找到第一次相遇的节点。

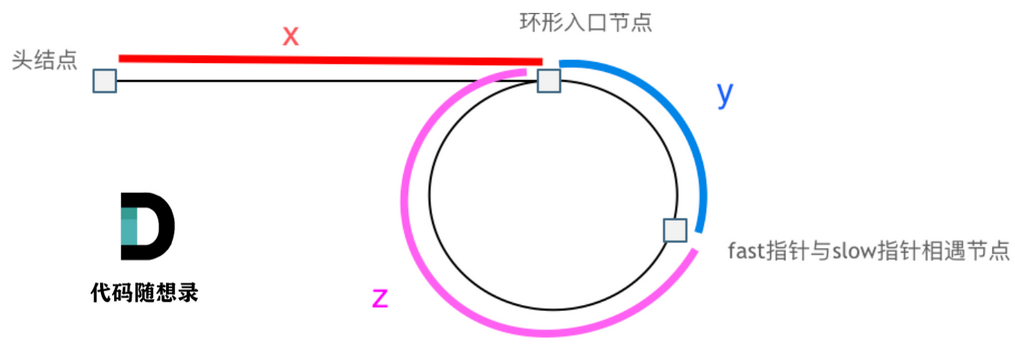
环形链表II.png

我们可以确定如下信息：

  • 慢指针必然不可能环绕圆形一圈，快指针至少环绕环形一圈
  • 快指针和慢指针从同一个起点出发，并且快指针是慢指针的两倍

设定 相应的变量之后，得到如下等式：n >= 1，且 n 为正整数 （因为快指针至少环绕环形一圈）

1
2
3
(x + y) * 2 = x + y + n ( y + z ) 
		↓
x = (n - 1)(x + y) + z

我们假定 n == 1，那么 x = z。这个时候再看图，就发现只要 快慢指针的相遇节点和头节点同时向前移动，它们两个的相遇点就是链表开始入环的第一个节点。

在完成《141.环形链表》题目的时候，我的第一份代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == NULL || head->next == NULL){
            return false;
        }
        ListNode* slow = head;
        ListNode* fast = head->next;
        while(fast != nullptr && fast->next != nullptr){
            if(slow == fast){
                return true;
            }
            slow = slow->next;
            fast = fast->next->next;
        }
        return false;
    }
};

我企图用这份代码来套用到本题，却发现犯了一个大错误，那就是 slow 和 fast 不是同一个起点开始，导致上面的推导公式失效。所以，我们务必保证最初的快慢指针的起点是一致的，即指向头节点。如果是这样，上面的代码还需要改正的地方是，要先进行指针移动，再判断快慢指针是否指向同一个节点，从而判断是否为环形链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool hasCycle(ListNode* head) {
        if (head == NULL || head->next == NULL) {
            return false;
        }
        
        ListNode* slow = head;
        ListNode* fast = head;
        while (fast != nullptr && fast->next != nullptr) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) { // 快慢指针，有环必相遇
                return true;
            }
        }
        return false;
    }
};