最小生成树的性质
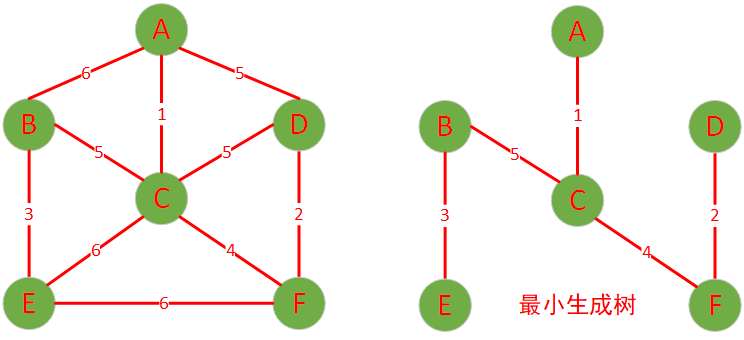image20250508130718977.png
克鲁斯卡尔算法（并查集）
基本思想：每次选取权值最小的边，加入生成树中，只要不构成环，直到所有点连通。
代码地址：克鲁斯卡尔算法
基本步骤
- 排序边：把图中所有的边按照权重从小到大进行排序，每次选择一条权重最小的边
- 初始化并查集：为图中的每个顶点创建一个独立的集合（创建一个并查集即可），用于后面判断加入边是否会形成环
- 选择边：从排序好的边列表中依次选取边，如果该边的两个顶点不在同一个集合（即加入这条变不会形成环），则将这条边加入最小生成树的边集，并将这两个顶点所在的集合合并
- 重复步骤 3：不断重复步骤 3，直到最小生成树的边数到达 n -
1，此时就得到了图的最小生成树
为什么并查集可以判断是否有环？
假设我们尝试加入边 (0, 3)，并查集当前状态：
find(0) = 0find(3) = 3- 因为
0 ≠ 3，所以不成环，可以加入，并执行
union(0, 3) 把它们并在一起。
之后再来一条边 (3, 0)：
find(3) = 0find(0) = 0- 因为相同 →
表示已有路径相连，加这条边会成环，所以拒绝它。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| struct Edge {
int from;
int to;
int weight;
Edge(int from, int to, int weight) : from(from), to(to), weight(weight) {}
bool operator<(const Edge &other) const {
return weight > other.weight;
}
};
class UnionFind {
public:
explicit UnionFind(int size) : parent(size) {
for (int i = 0; i < size; ++i) {
parent[i] = i;
}
}
int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]);
}
return parent[x];
}
void merge(int x1, int x2) {
auto new_x1 = find(x1);
auto new_x2 = find(x2);
if (new_x1 != new_x2) {
parent[new_x1] = new_x2;
}
}
private:
vector<int> parent;
};
int kruskal(int n, priority_queue<Edge> &edges, list<Edge> &mst) {
UnionFind union_find(n);
int total_weight = 0;
while (!edges.empty()) {
auto item = edges.top();
edges.pop();
if (union_find.find(item.from) != union_find.find(item.to)) {
union_find.merge(item.from, item.to);
mst.push_back(item);
total_weight += item.weight;
if (mst.size() == n - 1) {
break;
}
}
}
return total_weight;
}
|
示意图：
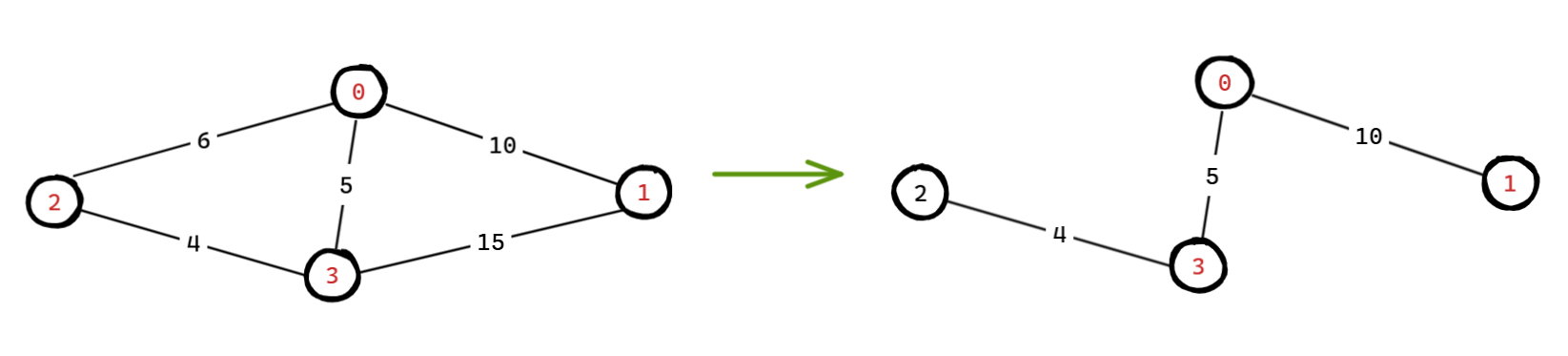image20250508150029093.png
为什么代码中必须判断当前边的数量是否等于
n - 1？
可以不判断，但效率低。
如果不加这句，程序会继续遍历所有边，即使已经找到了完整的最小生成树。
这
不会影响正确性，但会造成不必要的计算，尤其是在边很多（例如稠密图）时，效率会差很多。
普里姆算法
基本思想：从一个点出发，每次选择连接当前生成树和“外部”最近的一条边，直到所有点被包含在树中。
代码地址：普里姆算法
基本步骤
- 选择起始顶点：任意选择一个顶点作为起始点，将其加入最小生成树的顶点集合（用一个数组
visited[] 标记哪些点已经在生成树中）
- 选择最小边：使用优先队列维护当前顶点所有可以连接树的边，每次就从优先队列中取出权重最小的边，我们就可以拿到当前顶点（from）对应的另一个顶点（to）。如果这条边连接的点（to）还不在生成树中（没有被访问过），就加进去，并把这个点所有的出边加入优先队列中
- 重复步骤 3，直到所有点都加入生成树
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| struct Edge {
int from;
int to;
int weight;
Edge(int from, int to, int weight) : from(from), to(to), weight(weight) {}
bool operator<(const Edge &other) const {
return weight > other.weight;
}
};
int prim(int n, vector<vector<Edge>> &edges, list<Edge> &mst) {
vector<bool> visited(n, false);
int total_weight = 0;
visited[0] = true;
priority_queue<Edge> pq;
for (const Edge &e : edges[0]) {
pq.push(e);
}
while (!pq.empty()) {
auto [from, to, weight] = pq.top();
pq.pop();
if (visited[to]) continue;
mst.emplace_back(from, to, weight);
total_weight += weight;
visited[to] = true;
for (const auto &edge : edges[to]) {
if (!visited[edge.to]) {
pq.push(edge);
}
}
}
return total_weight;
}
|
示意图：
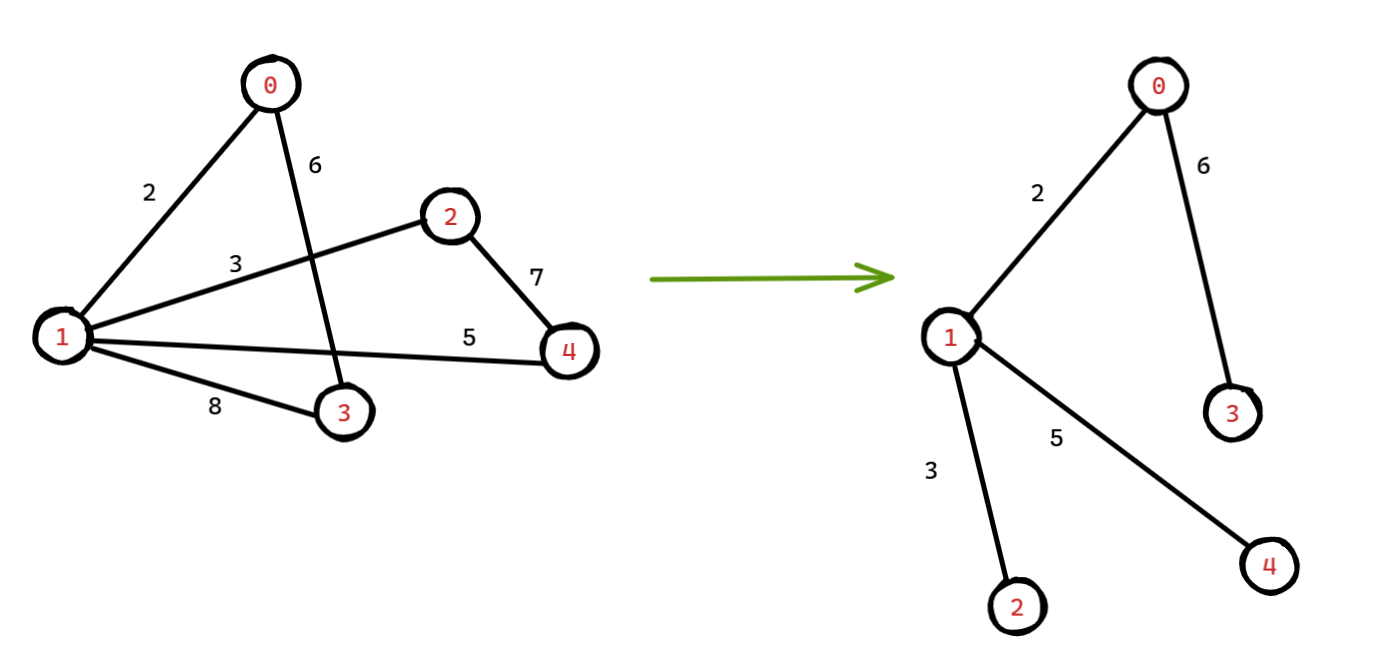image20250508150755351.png
两种算法的区别
| 特性/维度 |
Kruskal 算法 |
Prim 算法 |
| 思路核心 |
贪心选边：每次选最小边（不成环） |
贪心扩展点：从已选顶点延伸最小边 |
| 数据结构依赖 |
并查集（检测是否成环） |
优先队列（堆） + 访问标记 |
| 图结构依赖 |
边集（Edge List） |
邻接表或邻接矩阵 |
| 适合图类型 |
稀疏图（边少，节点多） |
稠密图（边多） |
| 边处理方式 |
全局排序后按权重选取边 |
从当前树延展，按权重扩展 |
| 终止条件 |
选满 n−1 条边 |
所有点都加入生成树 |
| 环路处理 |
用并查集避免构成环 |
用 visited 数组避免重复访问 |
| 灵活性 |
易用于处理离线边集、边是输入重点的图 |
更适合点-邻接结构清晰的网络拓扑、地图等场景 |
| 起点依赖性 |
与起点无关 |
与起点有关（不同起点结果结构可能不同） |
既可以应用于有向图，也可以应用于无向图？
不可以直接用于有向图。两者都主要用于无向图的最小生成树（MST）问题。
图的存储不同
Kruskal 算法 是以边为单位，而 Prim
算法 是以顶点为单位，两者在存储图结构的时候有所不同：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
vector<Edge> edges = {
{0, 1, 10},
{0, 2, 6},
{0, 3, 5},
{1, 3, 15},
{2, 3, 4}
};
graph[0].emplace_back(0, 1, 2);
graph[1].emplace_back(1, 0, 2);
graph[0].emplace_back(0, 3, 6);
graph[3].emplace_back(3, 0, 6);
|
树的结构可能不同，权重值不变
Kruskal 算法 ：树的结构确定，权重确定
Prim 算法 ：树的结构不确定，权重确定
Prim 算法选择不同的起始点，会导致树的结构不确定，但是 Kruskal 算法
的边的选择是唯一的。
