746. 使用最小花费爬楼梯
#动态规划 2025-01-21

70. 爬楼梯

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int climbStairs(int n) {
        if(n == 1) return 1;
        vector<int> dp(n);
        dp[0] = 1;
        dp[1] = 2;
        for(int i = 2; i < n; i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n - 1];
    }
};

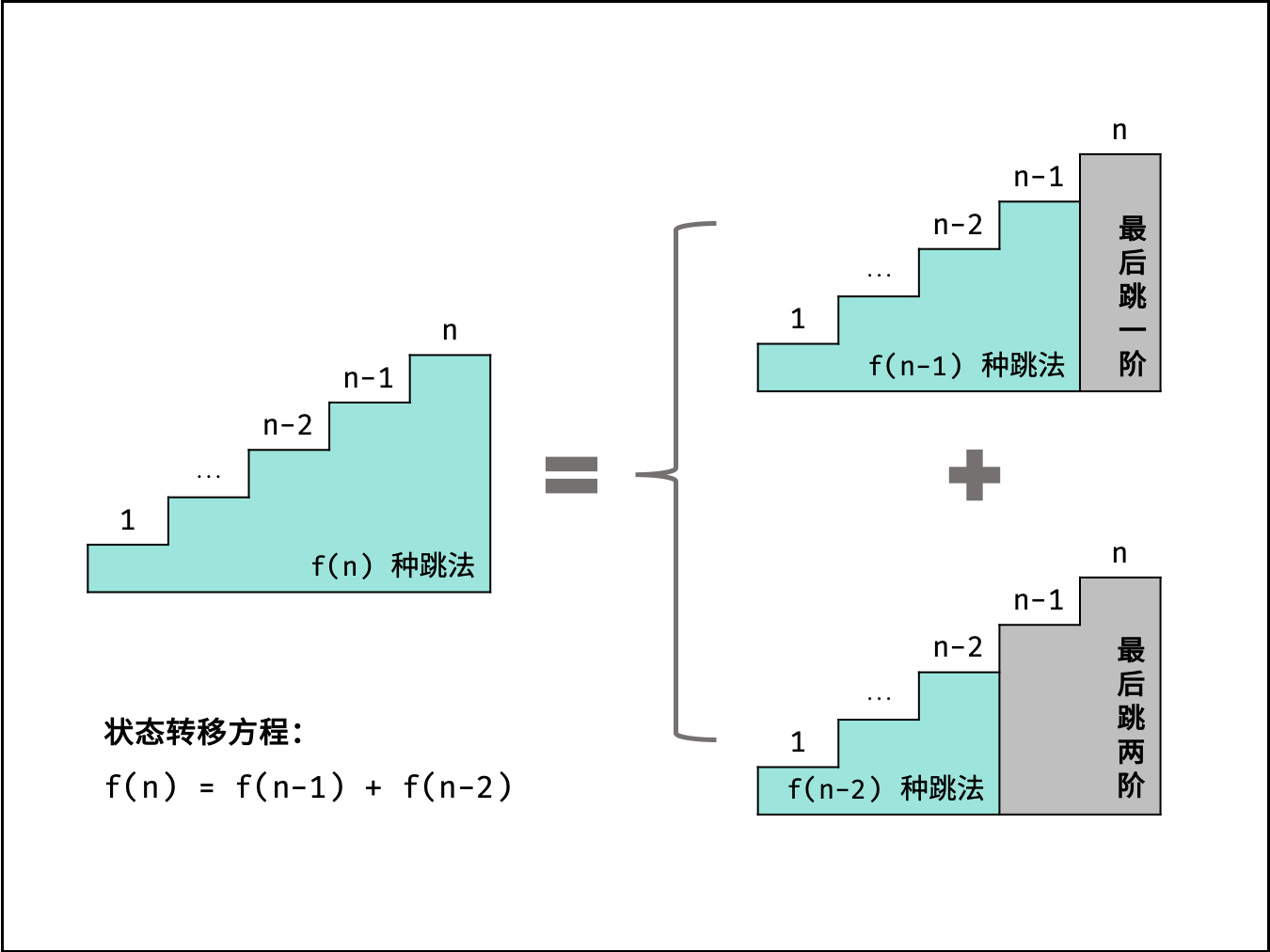
这道题有规律，即爬的楼梯的方式可由前面的爬楼梯的方式推导，也就是有一个公式：

b10133068165c0ad09195062a8f0a2f5.png

746. 使用最小花费爬楼梯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int size = cost.size();
        vector<int> dp(size);
        dp[0] = cost[0];
        dp[1] = cost[1];

        for(int i = 2; i < size; i++){
            dp[i] = min(dp[i - 1],dp[i - 2]) + cost[i];
        }

        return min(dp[size - 1],dp[size - 2]);
    }
};

当你计算到达楼梯 A 的花费，花费的金额就是出发的楼梯消费金额和到达的楼梯消费金额。

在一开始的时候，出发的楼梯消费金额计为0，初始化前两个楼梯 dp 消费金额为 dp[0] = cost[0] 和 dp[1] = cost[1]。

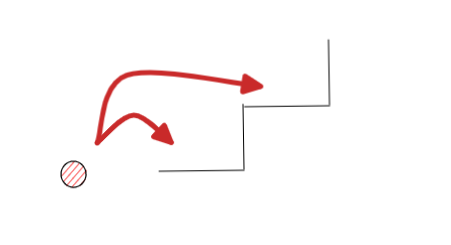image20250121171414077.png