303. 区域和检索 - 数组不可变
#前缀和与差分 2025-01-21 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class NumArray {
private:
    vector<int> find_data;
public:
    NumArray(vector<int>& nums) {
        find_data.clear();
        int size = nums.size();
        int prepare = 0;
        for(int i = 0; i < size; i++){  // 构建前缀和
            prepare += nums[i];
            find_data.push_back(prepare);
        }
    }

    int sumRange(int left, int right) {
        int sum;
        if(left == 0){
            sum = find_data[right];
        }else{
            sum = find_data[right] - find_data[left - 1];
        }
        return sum;
    }
};

前缀和在涉及计算区间和的问题时非常有用。

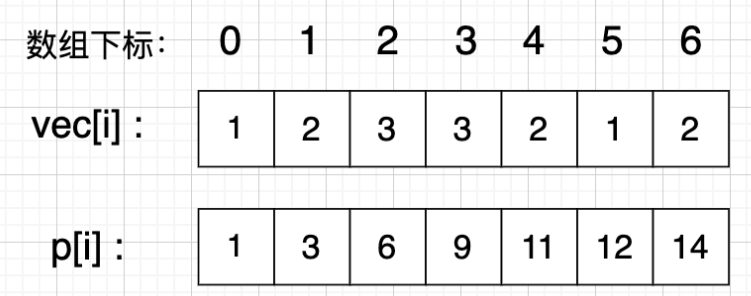
因为我这里构建前缀和的时候，并没有像有些人在构建前缀和那样，额外比原数组多一个空间来存储元素 0，就像下面这种：

1710e67ec95cef105f47551478d72620.png

正因为如此，sumRange 会有一个逻辑判断，当 left = 0 的时候，原来的计算公式 find_data[right] - find_data[left - 1] 就出现数组越界问题。

就算我们按照前面这个图片的构建前缀和思路来理解，带入这个公式计算 find_data[left - 1] 是为 0。因此按照我构建前缀和的那种思路来看，如果 left = 0，只需要返回 find_data[right] 即可，思路稍有差异，原理却是不变。

image20250121103633379.png